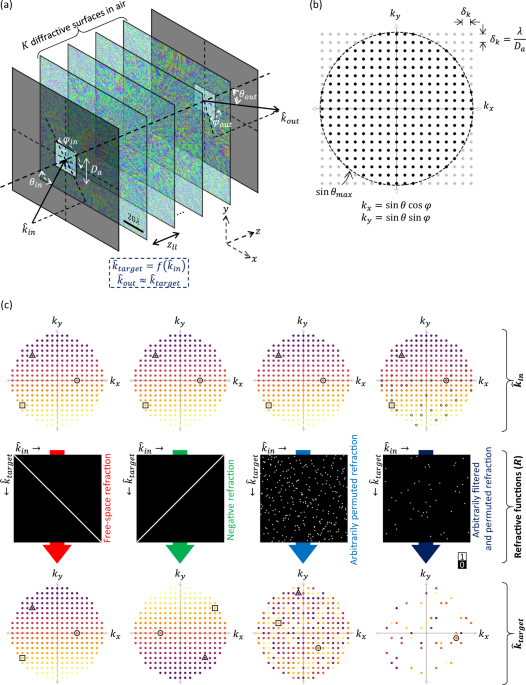
Programming of refractive functions

Nature Communications volume  16, Article number: 6896 (2025 ) Cite this article

Snell’s law dictates the phenomenon of light refraction at the interface between two media. Here, we demonstrate arbitrary programming of light refraction through an engineered material where the direction of the output wave can be set independently for different directions of the input wave, covering arbitrarily selected permutations of light refraction between the input and output apertures. Formed by a set of cascaded transmissive layers with optimized phase profiles, this refractive function generator (RFG) spans only a few tens of wavelengths in the axial direction. In addition to monochrome RFG designs, we also report wavelength-multiplexed refractive functions, where a distinct refractive function is implemented at each wavelength through the same engineered material volume, i.e., the permutation of light refraction is switched from one desired function to another function by changing the illumination wavelength. As experimental proofs of concept, we demonstrate permutation and negative refractive functions at the terahertz part of the spectrum using 3D-printed materials. Arbitrary programming of refractive functions enables new design capabilities for optical materials, devices and systems.

The study of refraction dates back to ancient times when early philosophers like Ptolemy explored the bending of light as it passed through different media. This bending is dictated by the Snell’s law, i.e., \({n}_{{in}}\sin {\theta }_{{in}}={n}_{{out}}\sin {\theta }_{{out}}\) , where \({n}_{{in}}\) and \({n}_{{out}}\) are the refractive indices of the two media, and \({\theta }_{{in}}\) and \({\theta }_{{out}}\) refer to the angles that the light rays have with respect to the surface normal, while the azimuthal angles of the incident and refracted rays remain the same, i.e., \({\varphi }_{{in}}={\varphi }_{{out}}\) 1,2. Advances in nanotechnology have enabled engineering of artificial materials3,4,5,6,7,8,9,10,11 with negative effective refractive indices12,13,14,15,16,17,18, causing light to bend in unusual ways and giving rise to phenomena such as anomalous refraction12,19,20,21,22,23,24 and perfect lensing25,26,27,28,29. However, the refractive function that relates the direction of the refracted wave \(\left({\theta }_{{out}},{\varphi }_{{out}}\right)\) to the direction of the incident wave \(\left({\theta }_{{in}},{\varphi }_{{in}}\right)\) is a fixed function determined by the refractive indices of the two media, as described by the Snell’s law. This behavior arises from the phase-matching condition30 of the wavefronts on both sides of an interface. Recognizing this fact allows the tuning of the refractive function along an interface by introducing a phase-gradient, leading to the generalized Snell’s law, \({n}_{{out}}\sin {\theta }_{{out}}-{n}_{{in}}\sin {\theta }_{{in}}=\frac{\lambda }{2\pi }\frac{d\psi }{{dx}}\) where \(\psi\) is the spatial phase distribution at the interface and λ is the wavelength of light31,32,33,34,35. Such a phase-gradient can be implemented by using, e.g., gradient metasurfaces, where the properties of the subwavelength inclusions constituting the meta-atoms vary gradually across a surface36,37,38,39,40,41,42,43. While there are reports of tunable refraction realized by adjusting the optical properties of these engineered materials through external stimuli44,45,46,47,48,49,50, at any given state of these materials, the behavior of light refraction for different input directions remains coupled. This prohibits arbitrary programming of the output wave direction independently for each input direction of light; as a result, arbitrary programming of refractive functions could not be achieved with these earlier designs.

Leave a Comment