Now that we have defined a secrecy system and discussed how to evaluate it, let us construct one based on the first and most important criterion, name

Perfect Secrecy

submited by

Style Pass

2024-12-12 14:30:01

Now that we have defined a secrecy system and discussed how to evaluate it, let us construct one based on the first and most important criterion, namely, a secrecy system that optimizes for secrecy i.e., a system that provides maximum secrecy. Such a secrecy system is called a perfectly secure system.

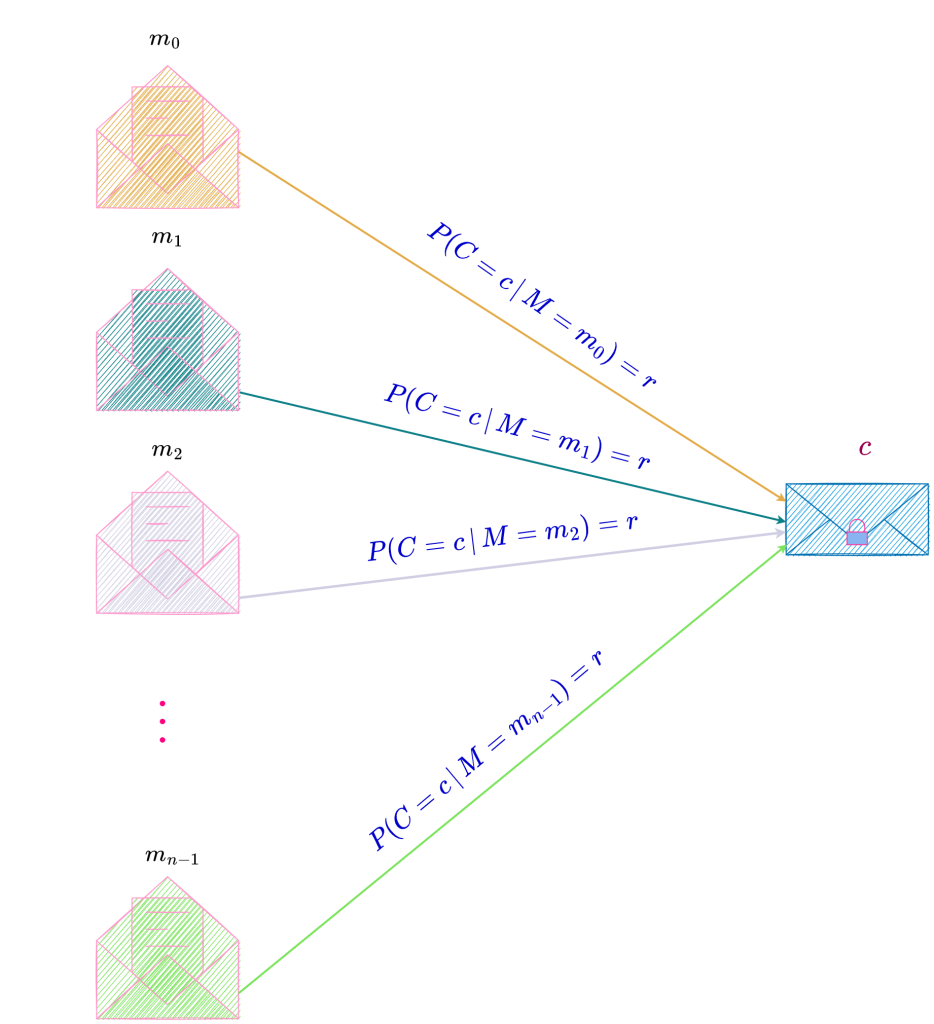
A secrecy system which is perfectly secure i.e., one which is maximally secure would provide no information about any of the messages it enciphers even if an adversary has unlimited time and computing resources to analyze any number of ciphertexts enciphered by the system.

Now that we have agreed on the defining characteristic of a perfectly secure secrecy system, let us translate this characteristic into mathematics and analyze the properties of such a secrecy system.

Let us assume that the possible messages m_0, m_1, \ldots, m_{n-1} (where n is the number of possible messages) are finite in number and their corresponding a priori probabilities are P(m_0), P(m_1), \ldots, P(m_{n-1}) and that these messages are enciphered into possible ciphertexts c_0, c_1, \ldots, c_{m-1} (where m is the number of possible ciphertexts) by