Fast Inverse Square Root

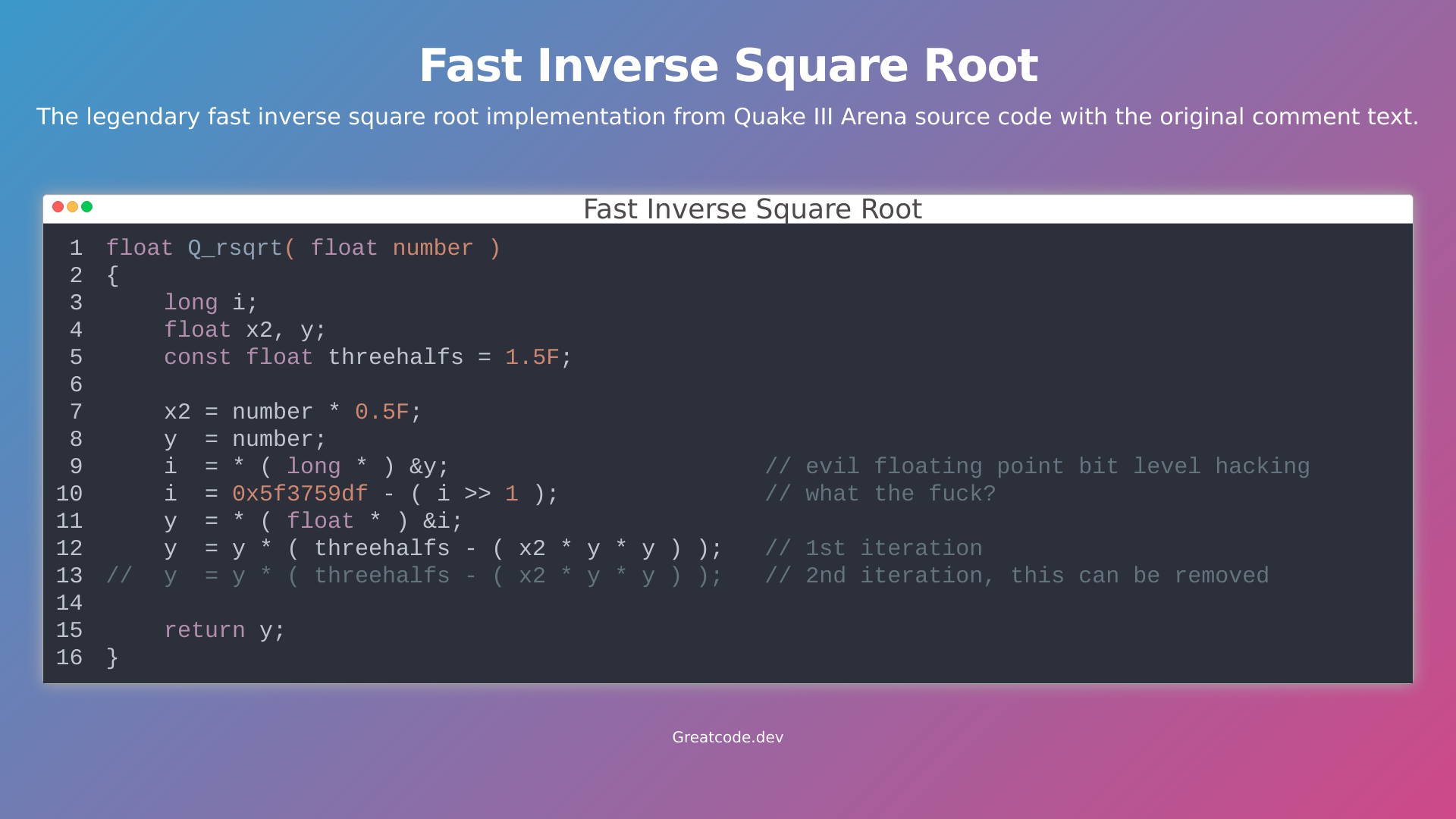
This code is an implementation of the inverse square root function (Q_rsqrt), which computes the reciprocal square root of a given float number. The function takes a float as an input and returns a float as output. The algorithm used in this implementation is known as the Fast Inverse Square Root algorithm, which was originally developed for the Quake III Arena game in 1999. It uses a clever bit manipulation trick to compute an approximation of the reciprocal square root in a very efficient way. The algorithm starts by taking the input number and dividing it by 2 to get x2. It then stores the original number in y and performs some bit-level hacking to convert the float representation of y into an integer. This is done to extract some of the bits from the floating-point representation of y, which will be used later in the algorithm. Next, the algorithm subtracts the integer representation of y shifted right by one from a magic number (0x5f3759df). This step is where the "what the fuck?" comment comes in, as it seems like a mysterious constant. However, this magic number was carefully chosen to improve the accuracy of the approximation. After this step, the algorithm converts the modified integer back into a float representation of y. It then performs a single iteration of Newton's method using the formula y = y * (threehalfs - x2 * y * y). This formula is derived from the Taylor series expansion of the reciprocal square root function. Finally, the function returns the computed value of y, which is an approximation of the reciprocal square root of the input number. The comment indicates that a second iteration can be performed, but it's not necessary for most use cases.

Leave a Comment